혼자 공부하는 머신러닝+딥러닝 / Chapter 03 회귀 알고리즘과 모델 규제

Chapter 03-1
k-최근접 이웃 회귀

 

- 회귀 (regression)

임의의 어떤 숫자를 예측하는 문제, 정해진 클래스가 없고 임의의 수치를 출력한다.

ex) 경제 성장률 예측, 배달이 도착할 시간 예측

 

- k-최근접 이웃 회귀

가장 가까운 샘플 k개를 선택하고 해당 수치들의 평균을 구함.

 

- 결정계수, R^2 (coefficient of determination)

회귀의 평가 점수

각 샘플의 타깃과 예측한 값의 차이를 제곱하여 더하고 타깃과 타깃 평균의 차이를 제곱하여 더한 값으로 나눈다.

예측이 타깃에 아주 가까워지면 1에 가까운 값이 된다.

 

코랩 실습 화면

 

import numpy as np

import matplotlib.pyplot as plt

from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsRegressor

from sklearn.metrics import mean_absolute_error

perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,

       21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,

       23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,

       27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,

       39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,

       44.0])

perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,

       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,

       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,

       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,

       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,

       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,

       1000.0])

# 산점도 (scatter)

plt.scatter(perch_length, perch_weight)

plt.xlabel('length')

plt.ylabel('weight')

plt.show()

# 훈련 세트, 테스트 세트로 나누기 (train_test_split)

# 사이킷런에 사용할 훈련 세트는 2차원 배열이어야 함

# 테스트 세트는 1차원으로 사용해도 된다.

train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)

# 수동으로 2차원 배열 만들기

# reshape() 사용, 원하는 크기 (ㅁ,ㅁ) 형식으로 전달

# 크기에 -1 지정시 나머지 원소 개수로 모두 채움 ex) .reshape(-1, 1)

test_array = np.array([1,2,3,4])

print(test_array)

test_array = test_array.reshape(2, 2)

print(test_array)

train_input = train_input.reshape(-1, 1)

test_input = test_input.reshape(-1, 1)

print(train_input.shape, test_input.shape)

# k-최근접 이웃 회귀 알고리즘 클래스

knr = KNeighborsRegressor()

# k-최근접 이웃 회귀 모델 훈련 (fit)

knr.fit(train_input, train_target)

# 테스트 세트 점수 확인 (score)

print('테스트 세트 점수: ', knr.score(test_input, test_target))

# 테스트 세트 예측 생성 (predict)

test_prediction = knr.predict(test_input)

# 테스트 세트의 평균 절댓값 오차 계산

# sklearn.metrics 패키지의 mean_absolute_error() 사용, 테스트 타겟과 예측값 전달

mae = mean_absolute_error(test_target, test_prediction)

print('테스트 세트의 평균 절댓값 오차 계산: ', mae)

 

- 출력 화면

 

[1 2 3 4]
[[1 2]
 [3 4]]
(42, 1) (14, 1)
테스트 세트 점수:  0.992809406101064
테스트 세트의 평균 절댓값 오차 계산:  19.157142857142862

 

- 과대적합 (overfitting)

훈련 세트에서 점수가 좋았는데 테스트 세트에서 점수가 나쁠 때 모델이 과대적합 되었다고 한다.

새로운 샘플에 대한 예측을 만들 때 잘 동작하지 않음

 

- 과소적합 (underfitting)

과대적합과 반대이거나 두 점수가 모두 낮을 때 과소적합이다.

또 다른 원인은 훈련 세트와 테스트 세트의 크기가 매우 작기 때문이다.

해결 방법은 모델을 조금 더 복잡하게 만들기-> 이웃의 개수를 줄이기

 

코랩 실습 화면

 

# 훈련 세트 점수 확인 (score)

print('훈련 세트 점수: ', knr.score(train_input, train_target))

# 과소적합 해결

# 이웃의 개수 줄이기 (모델을 더 복잡하게 만듬)

# n_neighbors 속성값 변경, 기본 5에서 3으로

knr.n_neighbors = 3

# 바뀐 이웃 개수로 모델 훈련 (fit)

knr.fit(train_input, train_target)

print('바뀐 이웃 개수의 훈련 세트 점수: ', knr.score(train_input, train_target))

# 테스트 세트 점수 확인 (score)

print("테스트 세트 점수", knr.score(test_input, test_target))

 

- 출력 화면

 

훈련 세트 점수: 0.9698823289099254

바뀐 이웃 개수의 훈련 세트 점수: 0.9804899950518966

테스트 세트 점수 0.9746459963987609

 

기본 미션
Ch.03(03-1) 2번 문제 출력 그래프 인증하기

코랩 실습 화면

 

# 확인문제 2번

# k-최근접 이웃 회귀 객체 생성

knr = KNeighborsRegressor()

# 5~45까지 x좌표 생성, 2차원으로

x = np.arange(5, 45).reshape(-1, 1)

# k값이 1, 5, 10일 때 예측 결과

for n in [1, 5, 10]:

  knr.n_neighbors = n

  # 모델 훈련

  knr.fit(train_input, train_target)

  # x 예측

  prediction = knr.predict(x)

  # 산점도

  plt.scatter(train_input, train_target)

  plt.plot(x, prediction)

  plt.title('n_neighbors = {}'.format(n))

  plt.xlabel('length')

  plt.ylabel('weight')

  plt.show()

 

- 출력 화면

 

 

 

 

 

 

Chapter 03-2
선형 회귀

 

- 선형 회귀 (linear regression)

대표적인 회귀 알고리즘, 어떤 직선을 학습하는 알고리즘여기서 직선은 특성을 가장 잘 나타낼 수 있는 직선사이킷런의 LinearRegression 클래스로 선형 회귀 알고리즘 생성

직선을 그리려면 y = ax + b의 형태 (a는 기울기 b는 절편)

 

coef_: 기울기 값

intercept_: 절편 값

 

코랩 실습 화면

 

import numpy as np

from sklearn.model_selection import train_test_split

from sklearn.neighbors import KNeighborsRegressor

import matplotlib.pyplot as plt

from sklearn.linear_model import LinearRegression

perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,

       21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,

       23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,

       27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,

       39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,

       44.0])

perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,

       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,

       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,

       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,

       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,

       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,

       1000.0])

# 훈련, 테스트 세트로 나누기 (train_test_split)

train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)

# 훈련, 테스트 input 2차원으로 변경 (reshape)

train_input = train_input.reshape(-1, 1)

test_input = test_input.reshape(-1, 1)

# k-최근접 이웃 회귀 모델 생성

knr = KNeighborsRegressor(n_neighbors=3)

# 모델 훈련 (fit)

knr.fit(train_input, train_target)

# 50cm 농어의 무게 예측 (predict, 리스트안의 리스트로 값 전달)

print('50cm 농어의 무게 예측: ', knr.predict([[50]]))

# 50cm 농어의 이웃 구하기 (kneighbors, 가장 가까운 이웃의 거리와 인덱스 반환)

distances, indexes = knr.kneighbors([[50]])

print('50cm 농어 이웃의 거리: ', distances, '인덱스: ', indexes)

# 산점도 (scatter)

plt.scatter(train_input, train_target)

# 50cm 농어의 이웃 표시

plt.scatter(train_input[indexes], train_target[indexes], marker='D')

# 50cm 농어 표시

plt.scatter(50, 1033, marker='^')

plt.xlabel('length')

plt.ylabel('weight')

plt.show()

# 이웃 샘플 타깃의 평균 (mean)

print('이웃 샘플 타깃의 평균: ', np.mean(train_target[indexes]))

# 새로운 샘플이 훈련 세트의 범위 벗어날 시 엉뚱한 값 예측

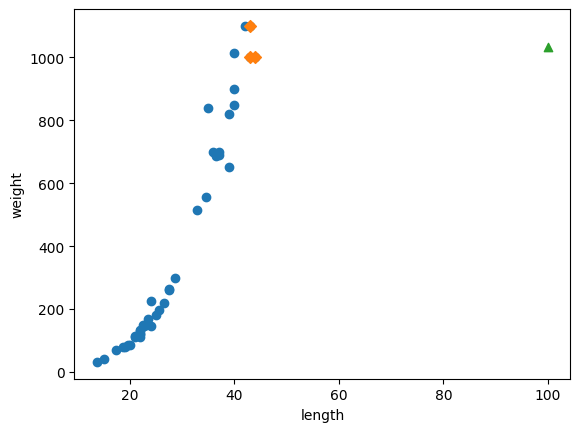
print('100cm 농어의 무게 예측: ', knr.predict([[100]]))

# 100cm 농어의 이웃 구하기 (kneighbors)

distances, indexes = knr.kneighbors([[100]])

print('100cm 농어 이웃의 거리: ', distances, '인덱스: ', indexes)

# 산점도 (scatter)

plt.scatter(train_input, train_target)

# 100cm 농어의 이웃 표시

plt.scatter(train_input[indexes], train_target[indexes], marker='D')

# 100cm 농어 표시

plt.scatter(100, 1033, marker='^')

plt.xlabel('length')

plt.ylabel('weight')

plt.show()

# 선형 회귀 모델 생성

lr = LinearRegression()

# 모델 훈련 (fit)

lr.fit(train_input, train_target)

# 50cm 농어 무게 예측 (predict)

print('50cm 농어 무게 예측: ', lr.predict([[50]]))

# 기울기와 절편 구하기

# coef_, intercept_ 사용

print('기울기: ', lr.coef_, '절편: ', lr.intercept_)

# 산점도 (scatter)

plt.scatter(train_input, train_target)

# 15~50까지 1차 방정식 그래프

plt.plot([15, 50], [15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_])

# 50cm 농어 데이터

plt.scatter(50, 1241.8, marker='^')

plt.xlabel('length')

plt.ylabel('weight')

plt.show()

# 훈련, 테스트 세트 점수

print('훈련 세트 점수: ', lr.score(train_input, train_target))

print('테스트 세트 점수: ', lr.score(test_input, test_target))

 

- 출력 화면

 

50cm 농어의 무게 예측:  [1033.33333333]
50cm 농어 이웃의 거리:  [[6. 7. 7.]] 인덱스:  [[34  8 14]]

이웃 샘플 타깃의 평균:  1033.3333333333333
100cm 농어의 무게 예측:  [1033.33333333]
100cm 농어 이웃의 거리:  [[56. 57. 57.]] 인덱스:  [[34  8 14]]

50cm 농어 무게 예측:  [1241.83860323]
기울기:  [39.01714496] 절편:  -709.0186449535477

훈련 세트 점수:  0.939846333997604
테스트 세트 점수:  0.8247503123313558

 

- 다항 회귀 (polynomial regression)

다항식을 사용한 선형 회귀

최적의 곡선 찾기

2차 방정식의 그래프를 그리려면 길이를 제곱한 항이 훈련 세트에 추가되어야 한다.

 

코랩 실습 화면

 

# 다항 회귀

# 최적의 곡선 찾기 (2차 방정식: ax제곱 + bx + c)

# 2차 방정식의 그래프를 그리려면 길이를 제곱한 항이 훈련 세트 데이터 앞에 추가되어야 함.

# 타깃값은 그대로 사용 (목표하는 값은 어떤 그래프를 훈련하든지 바꿀 필요 없음)

# 훈련 세트에 길이를 제곱한 항 추가 (column_stack)

train_poly = np.column_stack((train_input ** 2, train_input))

test_poly = np.column_stack((test_input ** 2, test_input))

# 위의 데이터셋 크기 확인

print(train_poly.shape, test_poly.shape)

# 선형 회귀 모델 생성

lr = LinearRegression()

# 모델 훈련 (fit)

lr.fit(train_poly, train_target)

# 50cm 농어 예측 (predict)

# 새로운 값 테스트할 때도 농어 길이의 제곱을 앞에 넣어줘야 한다.

print('50cm 농어 무게 예측: ', lr.predict([[50 ** 2, 50]]))

# 모델 기울기(계수), 절편 출력 (coef_, intercept_)

# 절편 [a b] 형태

print('기울기(계수): ', lr.coef_, '절편: ', lr.intercept_)

# 다항 회귀 그래프 그리기 (짧은 직선을 이어서 곡선처럼 표현)

# 구간별 직선을 그리기 위해 15~49까지 정수 배열 생성

point = np.arange(15, 50)

# 산점도 (scatter)

plt.scatter(train_input, train_target)

# 15~49까지 2차 방정식 그래프 생성 (plot)

# ax제곱 + bx + c, 여기서 point가 x값

plt.plot(point, 1.01 * point**2 - 21.6 * point + 116.05)

# 50cm 농어 데이터

plt.scatter(50, 1574, marker='^')

plt.xlabel('length')

plt.ylabel('weight')

plt.show()

# 훈련, 테스트 세트 점수

print('훈련 세트 점수: ', lr.score(train_poly, train_target))

print('테스트 세트 점수: ', lr.score(test_poly, test_target))

 

- 출력 화면

 

(42, 2) (14, 2)
50cm 농어 무게 예측:  [1573.98423528]
기울기(계수):  [  1.01433211 -21.55792498] 절편:  116.0502107827827

훈련 세트 점수:  0.9706807451768623
테스트 세트 점수:  0.9775935108325122

 

 

 

 

 

Chapter 03-3
특성 공학과 규제

 

- 다중 회귀 (multiple regression)

여러 개의 특성을 사용한 선형 회귀

1개의 특성 사용시 직선 학습, 2개의 특성 사용시 평면 학습

특성이 많은 고차원에서는 선형 회귀가 매우 복잡한 모델을 표현할 수 있다.

 

- 특성 공학 (feature engineering)

기존의 특성을 사용해 새로운 특성을 뽑아내는 작업

 

- 판다스 (pandas)

데이터 분석 라이브러리

 

- 데이터프레임 (dataframe)

판다스의 핵심 데이터 구조

넘파이와 비슷하지만 더 많은 기능 제공, CSV 파일 주로 사용

 

read_csv(): 주소를 전달하여 판다스로 읽기

to_numpy(): 넘파이 배열로 변경

 

코랩 실습 화면

 

import pandas as pd

import numpy as np

from sklearn.model_selection import train_test_split

from sklearn.preprocessing import PolynomialFeatures

from sklearn.linear_model import LinearRegression

from sklearn.preprocessing import StandardScaler

from sklearn.linear_model import Ridge

import matplotlib.pyplot as plt

from sklearn.linear_model import Lasso

# 데이터프레임 생성

# pd.read_csv() 사용, 주소 매개변수 값으로 전달

df = pd.read_csv('https://raw.githubusercontent.com/rickiepark/hg-mldl/master/perch_full.csv')

# 넘파이 배열로 변경

# to_numpy() 사용

perch_full = df.to_numpy()

print(perch_full)

perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,

       115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,

       150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,

       218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,

       556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,

       850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,

       1000.0])

# 훈련, 테스트 세트로 나누기 (train_test_split)

train_input, test_input, train_target, test_target = train_test_split(perch_full, perch_weight, random_state=42)

 

- 변환기 (transformer)

사이킷런에서 특성을 만들거나 전처리하기 위한 클래스

변환기는 타깃 데이터 없이 입력 데이터를 변환한다.

PolynomialFeatures 클래스 사용

 

transform(): 실제로 데이터 변환

get_feature_names_out(): 특성이 각각 어떤 입력의 조합으로 만들어졌는지 출력

 

코랩 실습 화면

 

# PolynomialFeatures 클래스 객체 생성

poly = PolynomialFeatures()

# 모델 훈련

poly.fit([[2,3]])

# 특성 변환

# transform 사용

print('2개의 특성 2와 3으로 이루어진 샘플: ', poly.transform([[2,3]]))

# 특성값 중 1 제거하기 위한 클래스 객체 생성

# 매개변수 include_bias=False 전달

poly = PolynomialFeatures(include_bias=False)

poly.fit([[2,3]])

print('2개의 특성 2와 3으로 이루어진 샘플 (특성중 1은 제거): ', poly.transform([[2,3]]))

# 훈련 세트 변환

poly = PolynomialFeatures(include_bias=False)

poly.fit(train_input)

train_poly = poly.transform(train_input)

print('train_poly 배열 크기: ', train_poly.shape)

# 각 특성이 어떤 조합으로 만들어졌는지 확인

# get_feature_names_out 사용

poly.get_feature_names_out()

# 테스트 세트 변환 (transform)

test_poly = poly.transform(test_input)

# 선형 회귀 모델 생성

lr = LinearRegression()

# 모델 훈련

lr.fit(train_poly, train_target)

print('훈련 세트 점수: ', lr.score(train_poly, train_target))

print('테스트 세트 점수: ', lr.score(test_poly, test_target))

# 특성 더 많이 추가하기 (고차항)

# degree= 매개변수로 차수 전달

poly = PolynomialFeatures(degree=5, include_bias=False)

poly.fit(train_input)  # 모델 훈련

# 특성 변환 (transform)

train_poly = poly.transform(train_input)

test_poly = poly.transform(test_input)

# 배열의 열의 개수가 특성의 개수

print('train_poly 배열 크기: ', train_poly.shape)

# 모델 훈련

lr.fit(train_poly, train_target)

print('훈련 세트 점수: ', lr.score(train_poly, train_target))

print('테스트 세트 점수: ', lr.score(test_poly, test_target))

 

- 출력 화면

 

2개의 특성 2와 3으로 이루어진 샘플: [[1. 2. 3. 4. 6. 9.]]

2개의 특성 2와 3으로 이루어진 샘플 (특성중 1은 제거): [[2. 3. 4. 6. 9.]]

train_poly 배열 크기: (42, 9)

훈련 세트 점수: 0.9903183436982125

테스트 세트 점수: 0.9714559911594111

train_poly 배열 크기: (42, 55)

훈련 세트 점수: 0.9999999999996433

테스트 세트 점수: -144.40579436844948

 

- 규제 (regularization)

모델이 훈련 세트에 과대적합되지 않도록 만드는 것

선형 회귀 모델의 경우 특성에 곱해지는 계수(기울기)의 크기를 작게 만드는 일

규제를 적용하기 전에 먼저 정규화부터 시행

 

- 릿지 회귀

규제가 있는 선형 회귀 모델

선형 모델의 계수를 작게 만들어 과대적합을 완화시킨다.

사이킷런의 Ridge() 클래스 사용

 

규제의 양은 alpha 매개변수로 조절

alpha 값이 크면 규제 강도가 세지므로 계수 값을 더 줄이고 과소적합 되도록 유도

적절한 alpha 값을 찾는 방법은 alpha 값에 대한 R^2 그레프를 그리는 것, 훈련 세트와 테스트 세트 점수가 가장 가까운 지점이 최적의 alpha 값이다.

 

- 라쏘 회귀

규제가 있는 선형 회귀 모델

릿지와 달리 계수 값을 아예 0으로 만들 수 있다.

사이킷런의 Lasso() 클래스 사용

 

코랩 실습 화면

 

# 특성의 스케일 정규화

# 사이킷런의 StandardScaler 클래스 객체 생성

ss = StandardScaler()

ss.fit(train_poly)  # 모델 훈련

# 특성 변환

train_scaled = ss.transform(train_poly)

test_scaled = ss.transform(test_poly)

# 릿지 (ridge) 모델 훈련

# 사이킷런의 Ridge 클래스 객체 생성

ridge = Ridge()

ridge.fit(train_scaled, train_target)  # 훈련

print('ridge 모델 훈련 세트 점수: ', ridge.score(train_scaled, train_target))

print('ridge 모델 테스트 세트 점수: ', ridge.score(test_scaled, test_target))

# 릿지와 라쏘 모델 사용시 규제의 양 조절

# alpha 매개변수 사용, alpha 값이 크면 규제 강도가 세지고 과소적합, 작으면 과대적합될 가능성

# score() 결과 저장할 리스트 생성

train_score = []

test_score = []

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:

  ridge = Ridge(alpha=alpha)  # 릿지 모델 생성

  ridge.fit(train_scaled, train_target)  # 릿지 모델 훈련

  # 훈련, 테스트 점수 저장

  train_score.append(ridge.score(train_scaled, train_target))

  test_score.append(ridge.score(test_scaled, test_target))

# 위의 그래프

plt.plot(np.log10(alpha_list), train_score)

plt.plot(np.log10(alpha_list), test_score)

plt.xlabel('alpha')

plt.ylabel('R^2')

plt.show()

# 구한 alpha 값으로 릿지 모델 훈련

ridge = Ridge(alpha=0.1)

ridge.fit(train_scaled, train_target)  # 훈련

print('릿지 훈련 세트 점수: ', ridge.score(train_scaled, train_target))

print('릿지 테스트 세트 점수: ', ridge.score(test_scaled, test_target))

# 라쏘 (Lasso) 모델 훈련

# 사이킷런의 Lasso 클래스 객체 생성

lasso = Lasso()

lasso.fit(train_scaled, train_target)  # 라쏘 모델 훈련

print('라쏘 훈련 세트 점수: ', lasso.score(train_scaled, train_target))

print('라쏘 테스트 세트 점수: ', lasso.score(test_scaled, test_target))

# 라쏘 모델의 alpha 값 찾기

train_score = []

test_score = []

alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:

  lasso = Lasso(alpha=alpha, max_iter=10000)  # 라쏘 모델 생성

  lasso.fit(train_scaled, train_target)  # 라쏘 모델 훈련

  # 훈련, 테스트 점수 저장

  train_score.append(lasso.score(train_scaled, train_target))

  test_score.append(lasso.score(test_scaled, test_target))

# 위의 그래프

plt.plot(np.log10(alpha_list), train_score)

plt.plot(np.log10(alpha_list), test_score)

plt.xlabel('alpha')

plt.ylabel('R^2')

plt.show()

# 구한 alpha 값으로 라쏘 모델 훈련

lasso = Lasso(alpha=10)

lasso.fit(train_scaled, train_target)  # 라쏘 모델 훈련

print('라쏘 훈련 세트 점수: ', lasso.score(train_scaled, train_target))

print('라쏘 테스트 세트 점수: ', lasso.score(test_scaled, test_target))

# 라쏘 모델의 계수 확인

# coef_ 사용

print('0인 계수의 개수: ', np.sum(lasso.coef_ == 0))

 

- 출력 화면

 

ridge 모델 훈련 세트 점수:  0.9896101671037343
ridge 모델 테스트 세트 점수:  0.9790693977615387

릿지 훈련 세트 점수:  0.9903815817570367
릿지 테스트 세트 점수:  0.9827976465386928
라쏘 훈련 세트 점수:  0.989789897208096
라쏘 테스트 세트 점수:  0.9800593698421883

라쏘 훈련 세트 점수:  0.9888067471131867
라쏘 테스트 세트 점수:  0.9824470598706695
0인 계수의 개수:  40

 

선택 미션
모델 파라미터에 대해 설명하기

 

머신러닝에서 사용되는 파라미터이다.

여기서 파라미터란 데이터들에 의해 결정되는 값을 말한다.

매개변수라고도 하며 모델 내부에서 결정되는 값이다.