Chapter 04-1
로지스틱 회귀
데이터프레임(dataframe): 판다스에서 제공하는 2차원 표 형식의 데이터 구조
데이터프레임에서 열을 선택하는 방법은 원하는 열을 리스트로 나열한다.
다중 분류(multi-class classification): 타깃 데이터에 2개 이상의 클래스가 포함된 문제
정렬된 타깃값은 classes_ 속성에 저장되어 있다.
- 함수 모음
unique(): 열에서 고유한 값을 추출하는 함수
proba(): 클래스별 확률값을 반환하는 메서드
코랩 실습 화면
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from scipy.special import expit
from scipy.special import softmax
fish.head() # 5개 행 출력
# 열의 고유값 출력
# unique() 사용
print("Species 열의 고유값: ", pd.unique(fish['Species']))
# 입력 데이터
# 데이터프레임에서 열 선택은 원하는 열을 리스트로 나열하기
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
print(fish_input[:5])
# 타깃 데이터
fish_target = fish['Species'].to_numpy()
# 훈련, 테스트 세트
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
# 훈련, 테스트 세트 전처리
ss = StandardScaler() # 모델 생성
ss.fit(train_input) # 훈련
train_scaled = ss.transform(train_input) # 변환
test_scaled = ss.transform(test_input) # 변환
# k-최근접 이웃 분류기의 확률 예측
kn = KNeighborsClassifier(n_neighbors=3) # 모델 생성
kn.fit(train_scaled, train_target) # 훈련
print("k-최근접 이웃 모델의 훈련 세트 점수: ", kn.score(train_scaled, train_target))
print("k-최근접 이웃 모델의 테스트 세트 점수: ", kn.score(test_scaled, test_target))
# KNeighborsClassifier에서 정렬된 타깃값 확인
# classes_ 속성 사용
print("k-최근접 이웃 모델에서 정렬된 타깃값: ", kn.classes_)
# 타깃값 예측 (predict)
print("테스트 세트 샘플의 타깃값 예측: ", kn.predict(test_scaled[:5]))
# 타깃값 확률 출력
# predict_proba() 사용
proba = kn.predict_proba(test_scaled[:5])
print("테스트 세트 샘플의 타깃값 확률: \n", np.round(proba, decimals=4))
# 이웃 클래스 확인
distances, indexes = kn.kneighbors(test_scaled[3:4])
print("네번째 샘플의 이웃: ", train_target[indexes])
- 출력 화면
Species 열의 고유값: ['Bream' 'Roach' 'Whitefish' 'Parkki' 'Perch' 'Pike' 'Smelt']
[[242. 25.4 30. 11.52 4.02 ]
[290. 26.3 31.2 12.48 4.3056]
[340. 26.5 31.1 12.3778 4.6961]
[363. 29. 33.5 12.73 4.4555]
[430. 29. 34. 12.444 5.134 ]]
k-최근접 이웃 모델의 훈련 세트 점수: 0.8907563025210085
k-최근접 이웃 모델의 테스트 세트 점수: 0.85
k-최근접 이웃 모델에서 정렬된 타깃값: ['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
테스트 세트 샘플의 타깃값 예측: ['Perch' 'Smelt' 'Pike' 'Perch' 'Perch']
테스트 세트 샘플의 타깃값 확률:
[[0. 0. 1. 0. 0. 0. 0. ]
[0. 0. 0. 0. 0. 1. 0. ]
[0. 0. 0. 1. 0. 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]
[0. 0. 0.6667 0. 0.3333 0. 0. ]]
네번째 샘플의 이웃: [['Roach' 'Perch' 'Perch']]
로지스틱 회귀(logistic regression): 선형 방정식을 학습하는 분류 모델
선형 방정식은 z = a * (Weight) + b * (Length) + c * (Diagonal) + d * (Height) + e * (Width) + f
에서 a, b, c, d, e는 가중치 혹은 계수이다.
z는 어떤 값도 가능하다. 하지만 확률이 되려면 0~1 사이 값이 되어야 한다.
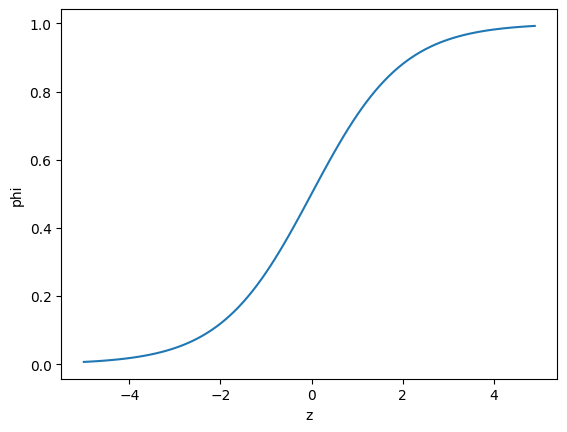
그럴려면 시그모이드 함수(sigmoid function) 또는 로지스틱 함수(logistic function)를 사용하면 가능하다.
이진 분류일 경우 시그모이드 함수의 출력이 0.5보다 크면 양성 클래스, 0.5보다 작으면 음성 클래스로 판단한다.
불리언 인덱싱(boolean indexing): 넘파이 배열에서 True, False 값을 전달하여 행을 선택하는 것
- 함수 모음
np.exp(): 지수 함수 계산
decision_function(): z 값 출력
expit(): 사이파이(scipy) 라이브러리의 시그모이드 함수
predict_proba(): 음성 클래스와 양성 클래스에 대한 확률 출력
softmax(): z 값을 확률로 변환
코랩 실습 화면
# 시그모이드 함수 그래프
# 지수 함수 계산은 np.exp() 사용
z = np.arange(-5, 5, 0.1)
phi = 1 / (1 + np.exp(-z))
plt.plot(z, phi)
plt.xlabel('z')
plt.ylabel('phi')
plt.show()
# 로지스틱 회귀로 이진 분류 수행 (불리언 인덱싱)
char_arr = np.array(['A', 'B', 'C', 'D', 'E'])
print("불리언 인덱싱으로 A, C 출력: ", char_arr[[True, False, True, False, False]])
# 불리언 인덱싱으로 도미와 빙어 행만 골라내기
bream_smelt_indexes = (train_target == 'Bream') | (train_target == 'Smelt')
train_bream_smelt = train_scaled[bream_smelt_indexes]
target_bream_smelt = train_target[bream_smelt_indexes]
# 로지스틱 회귀 모델의 예측
lr = LogisticRegression() # 모델 생성
lr.fit(train_bream_smelt, target_bream_smelt) # 훈련
print("로지스틱 회귀 모델의 타깃값 예측: ", lr.predict(train_bream_smelt[:5]))
print("로지스틱 회귀 모델의 타깃값 확률: \n", lr.predict_proba(train_bream_smelt[:5]))
print(lr.classes_)
print("로지스틱 회귀가 학습한 계수: ", lr.coef_, lr.intercept_)
# 로지스틱 회귀 모델의 z값 구하기
# decision_function() 사용
decisions = lr.decision_function(train_bream_smelt[:5])
print("로지스틱 회귀 모델의 z값: ", decisions)
# z값으로 확률구하기
# expit() 사용
print("확률: ", expit(decisions))
# 로지스틱 회귀로 다중 분류 수행
# C 매개변수로 규제 제어, max_iter 매개변수로 반복 횟수 지정
lr = LogisticRegression(C=20, max_iter=1000) # 모델 생성
lr.fit(train_scaled, train_target) # 훈련
print("로지스틱 회귀 모델의 훈련 세트 점수: ", lr.score(train_scaled, train_target))
print("로지스틱 회귀 모델의 테스트 세트 점수: ", lr.score(test_scaled, test_target))
print("로지스틱 회귀 모델의 타깃값 예측: ", lr.predict(test_scaled[:5]))
proba = lr.predict_proba(test_scaled[:5])
print("로지스틱 회귀 모델의 타깃값 확률: \n", np.round(proba, decimals=3))
print("로지스틱 회귀 모델의 클래스: ", lr.classes_)
print("로지스틱 회귀가 학습한 계수의 크기: ", lr.coef_.shape, lr.intercept_.shape)
# 로지스틱 회귀 모델의 z값 구하기
decision = lr.decision_function(test_scaled[:5])
print("로지스틱 회귀 모델의 z값: \n", np.round(decision, decimals=2))
# z값으로 확률구하기
# softmax() 사용, axis 매개변수 1로 지정하여 각 행에 대해 계산
proba = softmax(decision, axis=1)
print("확률: \n", np.round(proba, decimals=3))
- 출력 화면
불리언 인덱싱으로 A, C 출력: ['A' 'C']
로지스틱 회귀 모델의 타깃값 예측: ['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
로지스틱 회귀 모델의 타깃값 확률:
[[0.99759855 0.00240145]
[0.02735183 0.97264817]
[0.99486072 0.00513928]
[0.98584202 0.01415798]
[0.99767269 0.00232731]]
['Bream' 'Smelt']
로지스틱 회귀가 학습한 계수: [[-0.4037798 -0.57620209 -0.66280298 -1.01290277 -0.73168947]] [-2.16155132]
로지스틱 회귀 모델의 z값: [-6.02927744 3.57123907 -5.26568906 -4.24321775 -6.0607117 ]
확률: [0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]
로지스틱 회귀 모델의 훈련 세트 점수: 0.9327731092436975
로지스틱 회귀 모델의 테스트 세트 점수: 0.925
로지스틱 회귀 모델의 타깃값 예측: ['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
로지스틱 회귀 모델의 타깃값 확률:
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
로지스틱 회귀 모델의 클래스: ['Bream' 'Parkki' 'Perch' 'Pike' 'Roach' 'Smelt' 'Whitefish']
로지스틱 회귀가 학습한 계수의 크기: (7, 5) (7,)
로지스틱 회귀 모델의 z값:
[[ -6.5 1.03 5.16 -2.73 3.34 0.33 -0.63]
[-10.86 1.93 4.77 -2.4 2.98 7.84 -4.26]
[ -4.34 -6.23 3.17 6.49 2.36 2.42 -3.87]
[ -0.68 0.45 2.65 -1.19 3.26 -5.75 1.26]
[ -6.4 -1.99 5.82 -0.11 3.5 -0.11 -0.71]]
확률:
[[0. 0.014 0.841 0. 0.136 0.007 0.003]
[0. 0.003 0.044 0. 0.007 0.946 0. ]
[0. 0. 0.034 0.935 0.015 0.016 0. ]
[0.011 0.034 0.306 0.007 0.567 0. 0.076]
[0. 0. 0.904 0.002 0.089 0.002 0.001]]
기본 미션
Ch.04(04-1) 2번 문제 풀고, 풀이 과정 설명하기
문제: 로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는 무엇인가요?
답은 1번 시그모이드 함수 입니다.
이유는 이진 분류는 0과 1로 나눠지는데, 그 중 시그모이드 함수는 선형 방정식의 결과를 0과 1 사이의 값으로 압축하여 이진 분류에서 사용할 수 있기 때문입니다.
Chapter 04-2
확률적 경사 하강법
확률적 경사 하강법(Stochastic Gradient Descent): 점진적 학습 알고리즘
여기서 점진적 학습은 훈련한 모델을 버리지 않고 새로운 데이터에 대해서만 조금씩 더 훈련하는 학습 방법
가장 가파른 경사를 따라 원하는 지점에 조금씩 내려와서 도달하는 것이 목표이다. 경사는 연속적이어야 함.
딱 하나의 샘플을 훈련 세트에서 랜덤하게 골라 가장 가파른 길을 찾는다. 이것을 전체 샘플을 모두 사용할 때까지 계속한다.
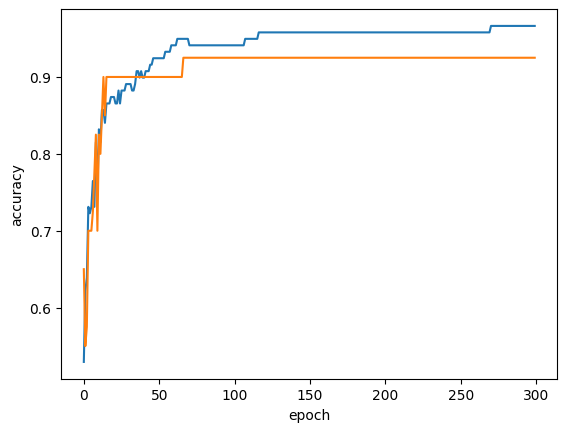
에포크(epoch): 훈련 세트를 한 번 모두 사용하는 과정, 경사하강법은 수십, 수백 번 이상 에포크 수행
미니배치 경사 하강법(minibatch gradient descent): 여러 개의 샘플을 사용해 경사 하강법을 수행하는 방식
배치 경사 하강법(batch gradient descent): 전체 샘플을 사용해 경사 하강법을 수행하는 방식
손실 함수(loss function): 어떤 문제에서 머신러닝 알고리즘이 얼마나 엉터리인지 측정하는 기준, 값이 작을수록 좋다.
비용 함수(cost function): 훈련 세트에 있는 모든 샘플에 대한 손실 함수의 합
로지스틱 손실 함수(logistic loss function) 또는 이진 크로스엔트로피 손실 함수(binary cross-entropy loss function):
이진 분류에서 사용하는 손실 함수
양성 클래스(타깃 1)일 때 손실을 -log(예측 확률)로 계산하고 확률이 0에 가까워질수록 손실은 큰 양수가 된다.
음성 클래스(타깃 0)일 때 손실은 -log(1-예측 확률)로 계산하고 예측 확률이 1에 가까워질수록 손실은 큰 양수가 된다.
크로스엔트로피 손실 함수(cross-entropy loss function): 다중 분류에서 사용하는 손실 함수
힌지 손실(hinge loss): 서포트 벡터 머신(support vector machine)이라 불리는 머신러닝 알고리즘을 위한 손실 함수
- 클래스 및 함수 모음
SGDClassifier 클래스: 확률적 경사 하강법 클래스, loss 매개변수는 손실 함수의 종류 지정하고 max_iter 매개변수는 수행할 에포크 횟수 지정
partial_fit(): 모델을 이어서 훈련할 때 해당 메서드 사용
코랩 실습 화면
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import SGDClassifier
import numpy as np
import matplotlib.pyplot as plt
# 입력, 타깃 데이터
fish_input = fish[['Weight', 'Length', 'Diagonal', 'Height', 'Width']].to_numpy()
fish_target = fish['Species'].to_numpy()
# 훈련, 테스트 세트
train_input, test_input, train_target, test_target = train_test_split(fish_input, fish_target, random_state=42)
# 데이터 전처리(훈련, 변환)
ss = StandardScaler()
ss.fit(train_input)
train_scaled = ss.transform(train_input)
test_scaled = ss.transform(test_input)
# 확률적 경사 하강법
sc = SGDClassifier(loss='log', max_iter=10, random_state=42)
sc.fit(train_scaled, train_target)
print('로지스틱 회귀 모델 훈련 점수: ', sc.score(train_scaled, train_target))
print('로지스틱 회귀 모델 테스트 점수: ', sc.score(test_scaled, test_target))
# 모델 이어서 훈련
# partial_fit() 사용
sc.partial_fit(train_scaled, train_target)
print('로지스틱 회귀 모델 훈련 점수: ', sc.score(train_scaled, train_target))
print('로지스틱 회귀 모델 테스트 점수: ', sc.score(test_scaled, test_target))
# 모델 이어서 300번의 훈련
sc = SGDClassifier(loss='log', random_state=42)
train_score = []
test_score = []
classes = np.unique(train_target)
for _ in range(0, 300):
sc.partial_fit(train_scaled, train_target, classes=classes)
train_score.append(sc.score(train_scaled, train_target))
test_score.append(sc.score(test_scaled, test_target))
# 위의 훈련 그래프
plt.plot(train_score)
plt.plot(test_score)
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
# 모델 100번 훈련
sc = SGDClassifier(loss='log', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print('훈련 100번의 훈련 점수: ', sc.score(train_scaled, train_target))
print('훈련 100번의 테스트 점수: ', sc.score(test_scaled, test_target))
# 힌지 손실을 사용한 모델 100번 훈련
sc = SGDClassifier(loss='hinge', max_iter=100, tol=None, random_state=42)
sc.fit(train_scaled, train_target)
print('힌지 손실을 사용한 훈련 점수: ', sc.score(train_scaled, train_target))
print('힌지 손실을 사용한 테스트 점수: ', sc.score(test_scaled, test_target))
- 출력 화면
확률적 경사 하강법 훈련 점수: 0.773109243697479
확률적 경사 하강법 테스트 점수: 0.775
확률적 경사 하강법 훈련 점수: 0.8151260504201681
확률적 경사 하강법 테스트 점수: 0.85
훈련 100번의 훈련 점수: 0.957983193277311
훈련 100번의 테스트 점수: 0.925
힌지 손실을 사용한 훈련 점수: 0.9495798319327731
힌지 손실을 사용한 테스트 점수: 0.925